시간복잡도와 공간복잡도
시간 복잡도와 공간 복잡도는 알고리즘 성능을 평가할 때 사용하는 개념으로 복잡도가 낮을수록 좋은 알고리즘이다.
시간 복잡도는 주어진 알고리즘이 문제를 해결하는 데 걸리는 시간입니다.
공간 복잡도는 주어진 알고리즘이 소비하는 메모리 양을 분석하는 방법입니다.
하지만 컴퓨터의 성능이 이전보다 좋아지고 저장 공간에 대해 걱정할 필요가 없기 때문에 중요성이 감소했습니다.
- 시간 복잡도
시간 복잡도를 고려한다는 것은 “입력 값의 변화에 따라 연산을 수행할 때 연산의 수에 비해 얼마나 많은 시간이 소요되는가?”를 의미합니다. 나는 그것이 말하는 것 같아요
즉, 효율적인 알고리즘을 구현한다는 것은 입력 값이 증가함에 따라 증가하는 시간의 비율을 최소화하는 알고리즘을 구성하는 것을 의미합니다.
– 시간 복잡도는 주로 ‘빅오 표기법‘는 최악의 경우를 고려하고 프로그램이 실행되는 데 걸리는 최악의 시간을 고려할 수 있기 때문에 사용됩니다.그때까지 걸릴 수 있습니다.” 대응 가능 - 공간 복잡성
공간복잡도는 시간복잡도와 반비례하는 경향이 있으며, 최근 대용량 시스템이 보편화되면서 알고리즘에서 시간복잡도가 공간복잡도보다 우선하는 경우가 있다.
스택
- 스택이란 무엇입니까?
스택의 사전적 의미와 같이 스택 형태의 데이터 구조를 말합니다. - 특성
동일한 구조와 크기의 데이터는 지정된 방향으로만 쌓일 수 있으며, 위에서 지정한 위치를 통해서만 접근이 가능합니다.
맨 위에 있는 데이터는 가장 최근에 입력된 데이터이며 삽입할 새 데이터는 맨 위에 있는 데이터 위에 쌓입니다. 데이터는 위에서만 삭제 및 추가가 가능하며, 아래 이미지와 같이 “Push”와 “Pop”을 통해 스택의 구조를
후입선출(LIFO) 구조라고 합니다.
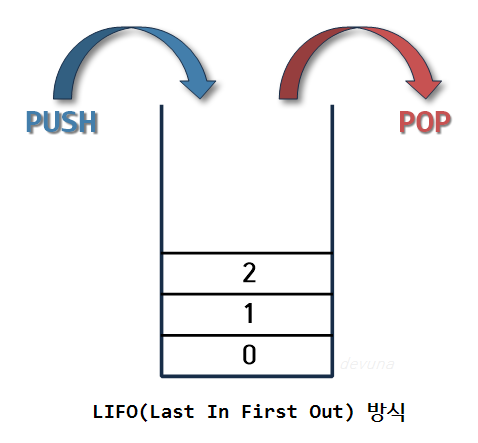
- 적용 예
– 웹 브라우저 검색 기록(뒤로): 마지막으로 열었던 페이지를 다시 표시합니다.
– 역순으로 문자열 만들기: 입력한 마지막 문자를 출력합니다.
– 실행 취소: 마지막 실행을 취소합니다.
– 후위 표기법 계산
– 수식의 괄호 검사(연산자 우선 표현을 위한 괄호 검사)
예어
- 대기열이란 무엇입니까?
고정된 상단에서 삽입과 삭제가 이루어지는 스택과 달리 한쪽 끝에서 삽입하고 다른 쪽 끝에서 삭제할 수 있는 양방향 구조입니다. - 특성
삭제 작업만 수행되는 곳을 전면, 삽입 작업만 수행되는 곳을 후면이라고 하며 각 작업만 수행합니다. 이때 뒤쪽에서 수행하는 삽입 작업을 enQueue라고 하고 앞쪽에서 수행하는 삭제 작업을 dnQueue라고 합니다. 대기열에서 앞 항목은 먼저 대기열에 들어간 첫 번째 항목입니다. - 적용 예
–우선 순위가 같은 작업 예약(인쇄기 프린터 대기열)
-은행업
– 콜센터 고객 대기시간
– 공정 관리
– 너비우선탐색(BFS) 구현
-캐시 구현# 개정 03/20 코드 비교
스택과 큐의 코드 비교
// 스택 var stack = new Stack(); stack.push(1); // 1 stack.push(3); // 2 stack.push(5); // 3 stack.pop(); // 5 stack.stackTop(); // 3 //큐 var queue = new Queue(); queue.enqueue(1); // 1 queue.enqueue(3); // 2 queue.enqueue(5); // 3 queue.dequeue(); // 1 queue.front(); // 3
